向量相似性检索及GPU加速调研

引言

随着人工智能和大数据的快速发展，向量检索已成为图像搜索、推荐系统、自然语言处理等领域的核心技术。在医疗病理学中，每张数字病理切片都蕴含大量微观信息，每段病理分析报告都包含高级语义信息，而现代AI技术（如UNI编码器[1]、MPNet[2]）可将这些图像或文本信息编码为高维向量（如1024维），形成可计算的语义空间，进而利用距离计算实现语义级搜索。向量检索（Vector Retrieval）作为这一过程的核心技术，能够根据相似性快速定位数据库中相似信息，为诊断决策、治疗方案推荐提供支持。然而，当数据规模达到千万甚至亿级时，传统的“暴力搜索”方法（逐一计算所有向量距离）耗时过长，难以满足临床实时性需求。

因此，如何高效索引与检索大规模向量数据成为关键问题。下文将由浅入深介绍向量检索技术，并探讨GPU加速在这一领域的核心价值。

向量检索基础

1. 数据向量化：从非结构化数据到语义空间

核心思想：让计算机“理解”非结构化数据

在医疗病理领域，无论是数字病理切片还是诊断报告文本，本质上都是非结构化数据——它们缺乏预定义的格式，但蕴含丰富的语义信息。为了使其可计算，我们需要通过**嵌入模型（Embedding Model）**将这些数据映射到高维向量空间，从而构建可量化的语义表达。

技术实现：

• 图像：使用深度神经网络（如ResNet[3]、ViT[4]）提取病理切片的形态学特征，输出固定长度的向量（例如1024维）。例如，乳腺癌的腺体结构、细胞核异型性等特征会被编码为向量中的特定维度激活值。
• 文本：通过Transformer模型（如BERT[5]、PubMedBERT[6]）将病理报告转化为向量。报告中“中分化腺癌”“淋巴转移”等关键术语会被编码为语义相近的向量方向。

一个好的嵌入模型应该能够做到对原始数据的语义保留，即相似病理特征的向量在空间中距离更近。例如，两张“肺腺癌”切片的向量相似度可能达到0.92，而“肺腺癌”与“肺鳞癌”的相似度可能仅为0.65。这里衡量两个向量的“相似度”时，通常采用的是欧氏距离（向量空间中两点的直线距离），此外，也可以选择其他常见的相似度或距离衡量指标如余弦相似度、点积等。

2. 相似性搜索：从KNNS到ANNS的演进

基本问题：给定查询向量，如何快速找到库中最相似的Top-K结果？

（1）传统KNNS方法的局限性

早期的相似性搜索主要依赖精确最近邻搜索（K-Nearest Neighbors Search, KNNS），其核心思路是通过构建索引结构加速计算，典型方法包括：

• KD-Tree[7]：基于数据维度递归划分空间（如n维向量的每个维度进行中位数或平均值划分），构建二叉树加速区域查询。
• Ball-Tree[8]：以超球体划分空间，利用球体间的包含关系快速排除无关区域。

然而，KNNS在医疗大规模数据场景中面临严重瓶颈：

• 维度限制：KD-Tree和Ball-Tree在面对高维向量（如数百维以上）时，会出现**维度灾难[9]，**递归划分和检索效率急剧下降。
• 动态更新缺陷：KD-Tree或Ball-Tree索引需静态数据支持，而医疗数据库需持续新增病例（如每日新增千例病理切片），由于无法动态插入数据，每次更新索引都需要重建KD-Tree，无法满足实时性需求。

（2）ANNS的近似性突破

为适应大规模高维度向量数据的高效检索，**近似最近邻搜索（Approximate Nearest Neighbor Search, ANNS）**通过可控的精度损失换取效率量级提升。

下文将具体介绍一些通用的主流向量索引技术，包括基于空间划分与量化技术的方法（IVFPQ[10])、基于图的检索方法（NN-Descent[11]、HNSW[12]）、基于GPU加速的检索方法（SONG[13]、CAGRA[14]）。

主流索引技术解析

1. IVFPQ

构造过程

IVFPQ（Inverted File Index with Product Quantization）[10]是一种结合空间划分与向量压缩的高效索引方法，其核心流程分为倒排索引构建（IVF）与乘积量化（PQ）两个阶段：

（1）倒排索引构建（IVF）

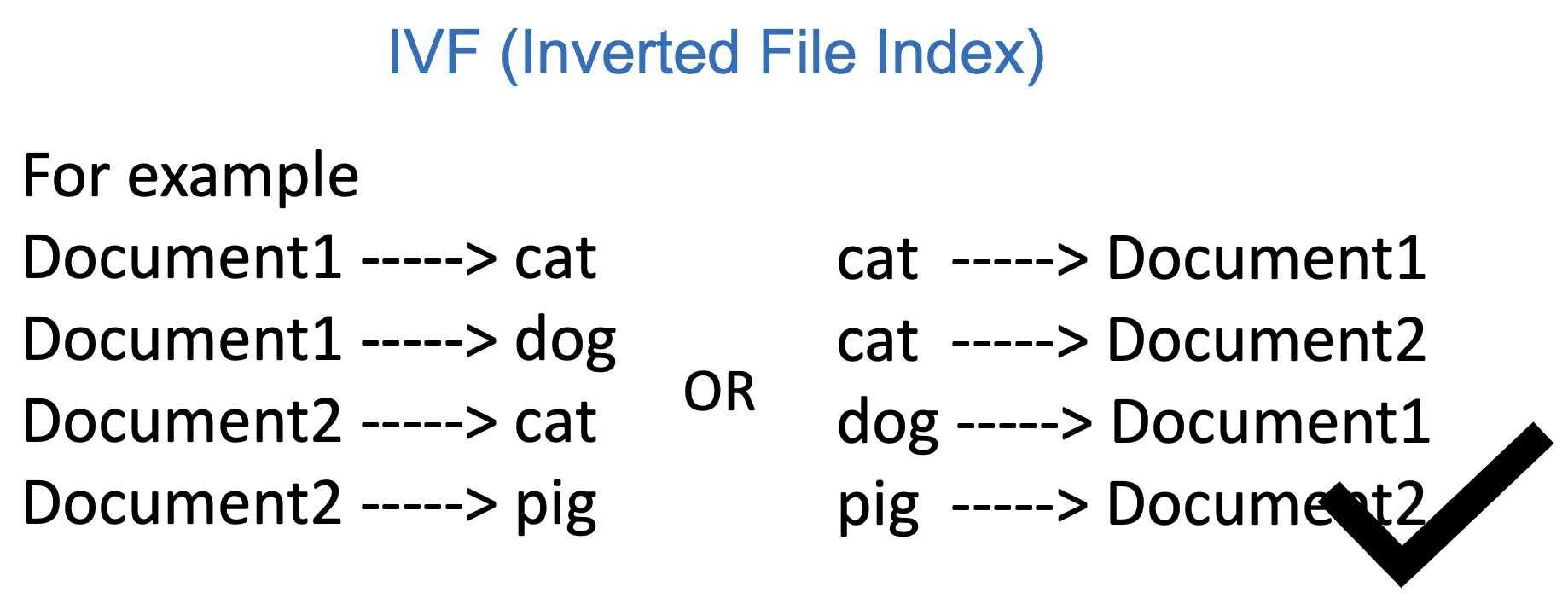
为了更好理解，下面以一个文档查询关键词的例子来说明IVF的作用，以图1左半部分为例，现有一堆文档，Document1、2、3、4，每个文档会有不同的单词内容，我们想要检索某个单词在哪些文档中出现过，比如dog，如果按一般逻辑去检索的话，要对每个文档的每个单词进行遍历，对每个单词进行判断是不是dog，来检查对应文档是不是包含dog，这种做法显然是很耗时的，极端情况下需要把所有文档所有单词都遍历一遍。

IVF就是换了一种思路，我们事先统计出来哪些单词存放在哪些文档里面，例如图1右半部分，我们记录每个单词对应了哪些文档，这样检索的时候只需要去找到这个单词的位置，就可以知道他在哪些文档里出现过，由于词表的长度往往比所有文档的长度要短，因此可以节省检索时间。

具体到向量检索场景中，基本的流程如下：

1. 聚类中心生成：使用K-Means算法对全量向量数据集​\mathcal{D} = \{v_1, v_2, ..., v_n\}进行聚类，生成​n_{\text{list}}个簇中心​C = \{c_1, c_2, ..., c_{n_{\text{list}}}\} 。
2. 倒排列表构建：对每个簇中心​ c_i ，记录其对应的成员向量集合​ \mathcal{L}_i = \{v_j | \arg\min_k \|v_j - c_k\|_2 = i\} ，形成倒排列表结构。
3. 参数意义：​ n_{\text{list}} 控制粗粒度聚类数量，其值越大则检索精度越高，但计算成本随之增加（默认值通常为1024）。

（2）乘积量化（PQ）

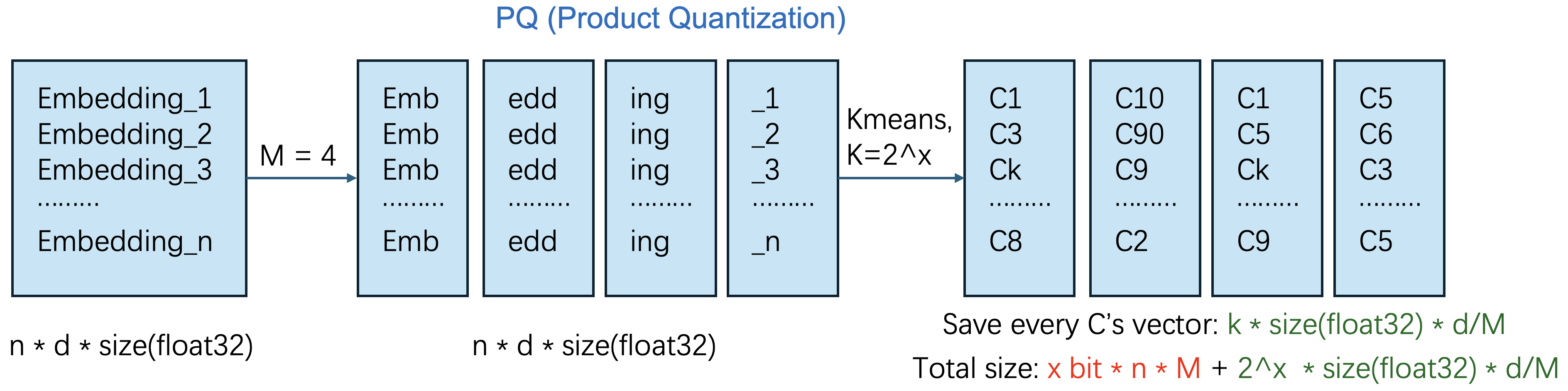
乘积量化的主要目的是为了减少内存占用，因为如果有非常多的向量的话，占用的内存也会很多，该方法是为了减少内存占用设计的，参考图2，具体的做法如下：

1. 向量分块：将原始向量​ v \in \mathbb{R}^d 划分为​ M 个子向量块​ v = [v^{(1)}, v^{(2)}, ..., v^{(M)}] ，每块维度为​ d/M 。
2. 子空间量化：对所有子空间​ \mathbb{R}^{d/M} 统一进行K-Means聚类，生成码本​ \mathcal{B}_m = \{b_{m,1}, b_{m,2}, ..., b_{m,2^x}\} ，其中​ x 为码本比特数（通常​ x=8 , ​ 2^x=256 ）。
3. 编码压缩：将原始向量​ v 替换为各子块对应的簇ID编码​ \text{code}(v) = [k_1, k_2, ..., k_M] ，其中​ k_m = \arg\min_j \|v^{(m)} - b_{m,j}\|_2 。

内存优化分析

量化后总存储量由两部分构成：

• 码本存储：​ M \times 2^x \times \frac{d}{M} \times \text{float32} = 2^x d \times \text{float32} 。
• 编码存储：​ n \times M \times x \text{ bits} 。

以​ d=1024 , ​ M=8 , ​ x=8 为例，原始存储需​ 1024 \times 4 = 4096 字节/向量，而PQ压缩后仅需​ 8 \times 8 = 64 比特（8字节），压缩率高达512倍。

检索机制

1. 粗粒度筛选（IVF阶段）：计算查询向量​ q 与所有簇中心​ c_i 的距离，选取最近邻的​ n_{\text{probe}} 个簇。
2. 细粒度计算（PQ阶段）：对候选簇​ \mathcal{L}*i 中的每个向量​ v_j ，利用预计算码本进行快速距离估计：

其中​ q^{(m)} 为查询向量的第​ m 个子块，​ b_{m, k_j^{(m)}} 为​ v_j 第​ m 子块对应的码本中心。

3. Top-K排序：按计算距离升序排序，返回全局前​ K 个最近邻向量。

2. NN-Descent

构造过程

NN-Descent（Nearest Neighbor Descent）[11]是一种基于局部图结构优化的近似近邻搜索算法，其核心思想是通过迭代优化动态调整邻居关系，逐步逼近真实​K近邻图。其构造过程可形式化描述如下：

（1）图初始化

1. 随机邻居采样：对每个数据点​v_i \in \mathcal{D}，随机选择​K个初始邻居​N^{(0)}(v_i)，构建初始有向近邻图​G_0。
2. 反向邻居索引：同时记录反向邻居关系​R(v_i) = \{v_j | v_i \in N^{(0)}(v_j)\}，形成双向连接结构。

（2）迭代优化

在第​t次迭代中，通过反向邻居传递与三角闭包性质优化邻居关系，以图3为例，在某一次迭代过程中，我们对a点，找到他所有的邻居和反向邻居，也就是b、c和d，然后对于其中的点c，再对c找他的所有邻居和反向邻居，也就是e和d，这时候我们计算a到e的距离，如果a和e的距离比从a到c再到e的距离短的话，便更新这个图，把ae连起来，具体的算法过程如下：

1. 候选集生成：

   对点​v_i，合并其邻居与反向邻居生成候选集：

   \mathcal{C}(v_i) = N^{(t)}(v_i) \cup \bigcup_{v_j \in N^{(t)}(v_i)} R(v_j)

2. 局部距离计算：

   计算​v_i与​\mathcal{C}(v_i)中所有候选点的距离，并筛选出距离更近的潜在邻居。

3. 邻居更新：

   对每个​v_j \in \mathcal{C}(v_i)，若​d(v_i, v_j) < \max_{v_k \in N^{(t)}(v_i)} d(v_i, v_k)，则将​v_j加入新邻居集​N^{(t+1)}(v_i)。

4. 度数约束：

   保留每个点​v_i的前​K个最近邻居，其余连接剪枝移除。

（3）收敛条件

当满足以下条件之一时终止迭代：

• 邻居更新比例低于阈值​\epsilon（如​\epsilon=0.01）
• 达到预设最大迭代次数​T_{\max}（如​T_{\max}=20）

检索机制

在构建完成的近邻图上，采用以下策略实现高效搜索：

1. 多起点并行搜索：

   从随机选取的​L个起始点（如​L=50）出发，并行执行贪婪爬山算法。

2. 动态候选列表维护：

   对每个搜索路径，维护动态候选队列​\mathcal{Q}，按距离排序保留前​K个候选点。

3. 邻居扩展策略：

   对当前最近点​v_{\text{curr}}，将其邻居集​N(v_{\text{curr}})加入​\mathcal{Q}，并更新距离排序。

4. 终止条件：

   当候选队列​\mathcal{Q}中的最小距离连续​\tau次迭代（如​\tau=3）未更新时终止搜索。

数学建模

设数据集​\mathcal{D}中任意两点的距离为​d(v_i, v_j)，算法通过最小化以下目标函数逼近真实K近邻图：

迭代优化过程可视为在局部区域内执行梯度下降，逐步降低​\mathcal{L}(G)。

3. HNSW

构造过程

HNSW（Hierarchical Navigable Small World）[12]是一种结合分层结构与可导航小世界图的高效索引方法，其核心设计灵感来源于自然界的蜂巢式网络与人类社交网络的多层拓扑特性。算法通过构建层级递减的图结构实现搜索路径的指数级缩短，具体流程如下：

（1）层级化图结构生成

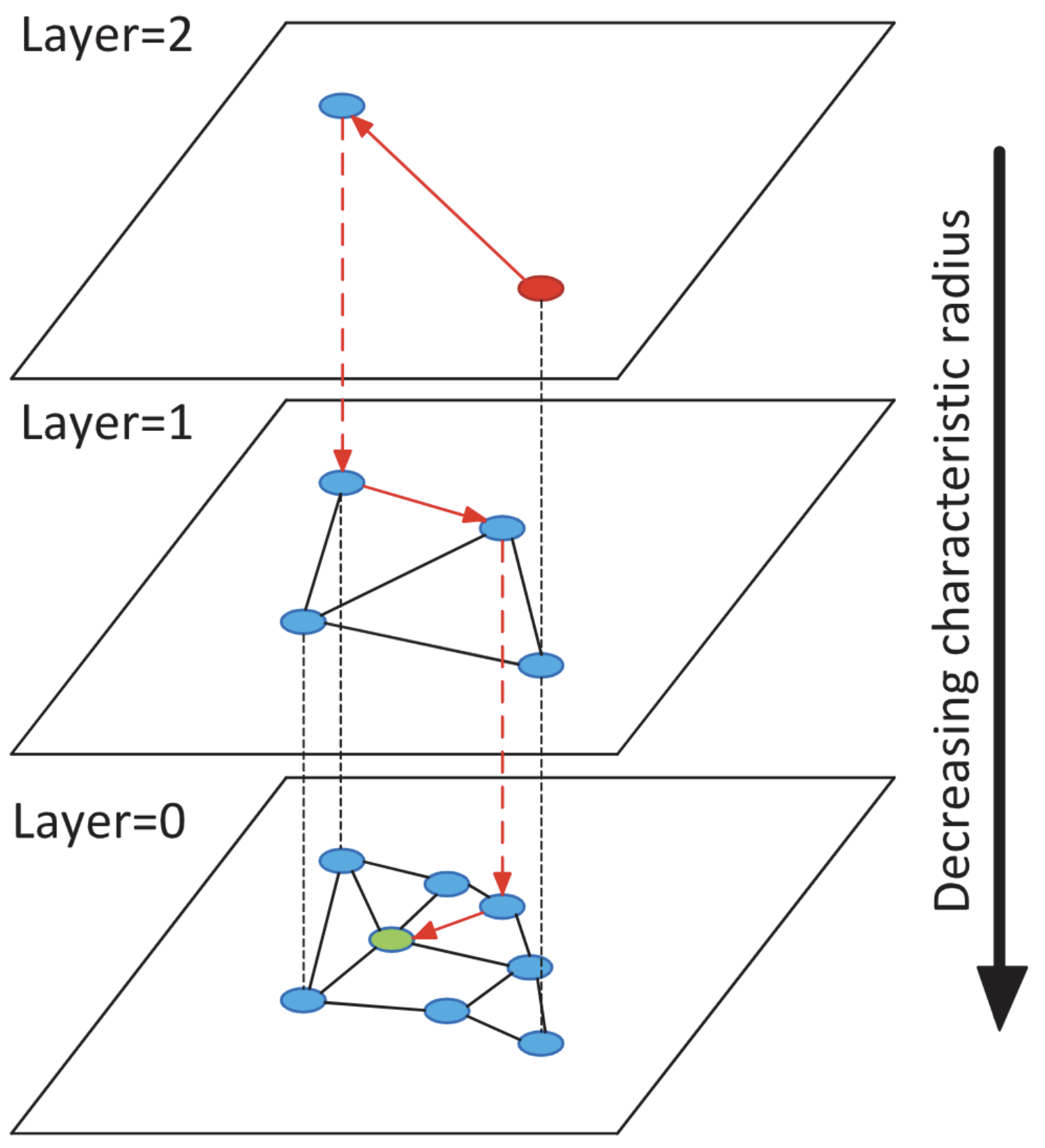
1. 概率分配层数：对每个数据点​v_i \in \mathcal{D}，随机分配最大层数​l_{\max}(v_i)，满足：

   l_{\max}(v_i) = \lfloor -\ln(\text{rand}(0,1)) \cdot m_L \rfloor

   其中​m_L为层间衰减系数（通常取​1/ln(M)，​M为每层最大连接数），此分配策略使得高层节点数量呈指数衰减。

2. 分层构建图：

   • 顶层构建（Layer L）：仅包含满足​l_{\max}(v_i) \geq L的节点，构成稀疏连接的小世界图。
   • 逐层向下扩展：在层​l中，节点包含所有满足​l_{\max}(v_i) \geq l的节点，且每个节点维护至多​M条双向边。

（2）动态插入策略

当新节点​v_{\text{new}}插入时，按以下规则逐层更新图结构（以层​l为例）：

1. 搜索当前层入口：从高层​L开始，使用贪心算法找到层​l中距离​v_{\text{new}}最近的入口点​e_l。

2. 局部邻域探索：在层​l中，以​e_l为起点，通过优先队列扩展候选集，保留距离​v_{\text{new}}最近的​ef_{\text{Construction}}个节点。

3. 连接优化：从候选集中选择至多​M个邻居，满足：

   • 距离最近原则：优先连接距离最近的节点。
   • 多样性约束：避免局部聚集，通过启发式算法选择方向差异较大的边（避免孤岛现象）。

检索机制

HNSW的搜索过程通过跳表式的逐层细化策略实现高效导航，具体步骤如下：

1. 顶层入口定位：

   • 从最高层​L的随机节点出发，执行贪心算法找到该层距离查询​q最近的节点​e_L。

2. 逐层下降搜索：

   从​e_L开始，根据层之间的跳表关系，在下一层​e_{L-1}的邻居中找到距离​q最近的一个邻居，并作为下一层的输入；

3. 底层精确检索：

   • 在层0中，从入口点​e_0出发，使用类似NN-Descent的动态候选列表算法：

     1. 初始化动态列表​\mathcal{C}，包含​e_0及其邻居。
     2. 迭代扩展​\mathcal{C}，维护前​ef_{\text{Search}}个最近邻。
     3. 当连续​\tau次迭代未更新最近邻时终止，返回Top-K结果。

4. SONG

设计动机

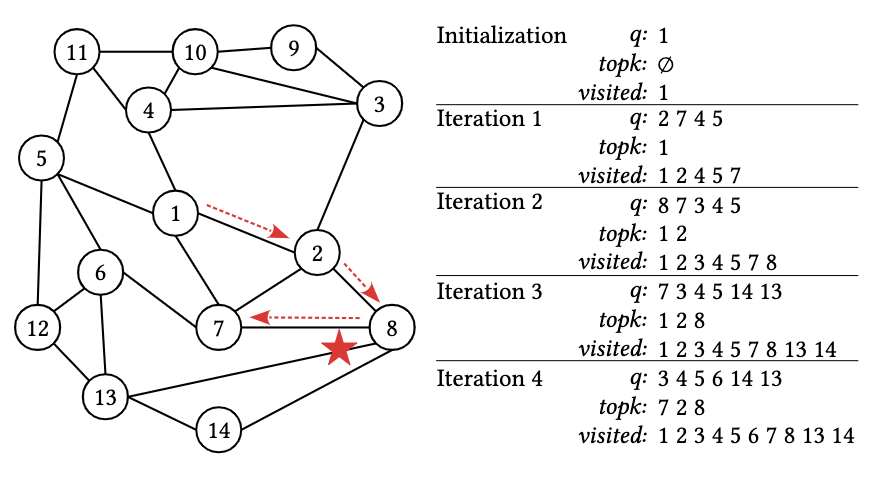
基于图的近似最近邻搜索（ANNS）通常依赖优先级队列、结果堆、访问记录表三个核心数据结构，其迭代式搜索流程在CPU上表现为串行逻辑：

1. 优先级队列（q）：维护待扩展的候选节点（按距离排序）
2. 结果堆（TopK）：保存当前最近的K个结果
3. 访问记录表（Visited）：标记已访问节点避免重复计算

以图5的搜索过程为例，传统方法需逐轮迭代：从队列中取出最近节点，计算其邻居距离，更新结果堆。然而，95%的计算时间消耗在高维向量距离计算（如1024维欧氏距离），而CPU的单线程架构无法并行处理这一过程。即使将查询任务并行化，单个复杂查询仍会阻塞整个流水线。

整体架构

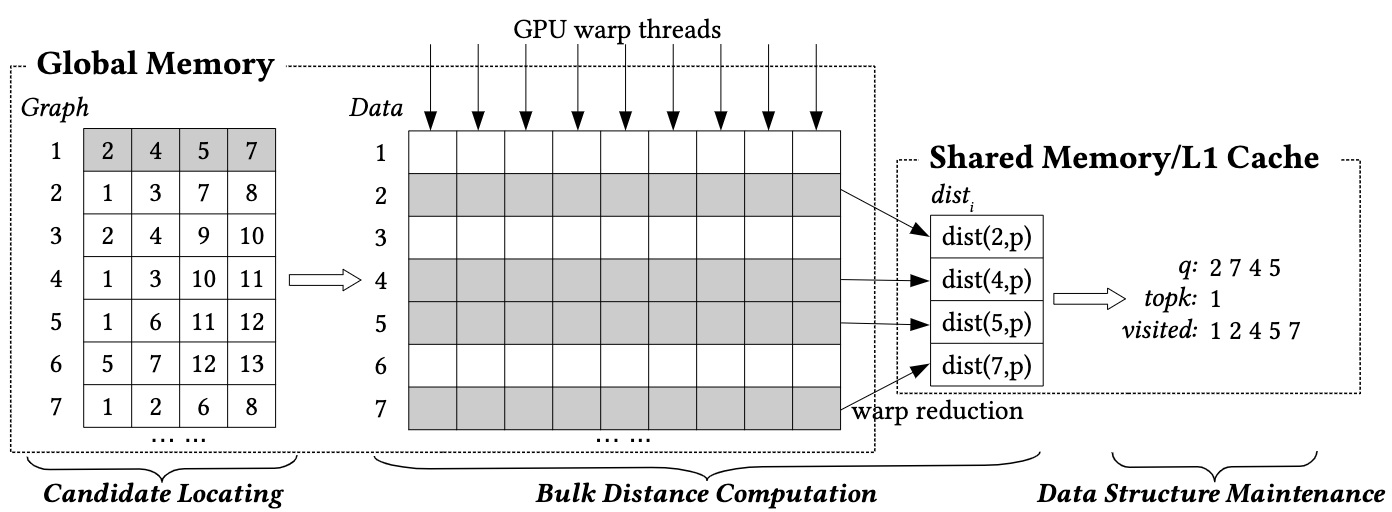
SONG[13]的核心创新在于重构搜索流水线，将串行步骤解耦为GPU友好的三阶段并行任务，如图6所示：

优化设计

1. 候选定位（Candidate Locating）

• 目标：从全局显存（Global Memory）中加载候选节点的邻居列表

• 优化策略：

  • 固定度数图存储：限制每个节点的邻居数量上限（如64），显存预分配连续空间，避免动态内存开销
  • 多查询批量加载：每个GPU线程组（Warp）同时处理多个查询的候选节点

2. 批量距离计算（Bulk Distance Computation）

• 并行化核心：将高维向量计算分解为GPU线程级任务

  • 公式：欧氏距离​d(q,v)=\sqrt{\sum_{i=1}^{d}(q_i-v_i)^2}被拆分为​d个并行减法-平方操作，通过Warp内线程协同规约求和
  • 显存对齐访问：同一节点的向量数据连续存储，单次读取128字节（GPU缓存行）

3. 数据结构更新（Data Structure Update）

• 轻量级原子操作：单个线程负责更新队列、结果堆和访问记录
• TopK堆压缩：仅保留距离最近的K个结果，堆容量固定为​K_{\max}（如K=100）
• Cuckoo Filter[15]替代哈希表：支持动态插入与删除

5. CAGRA

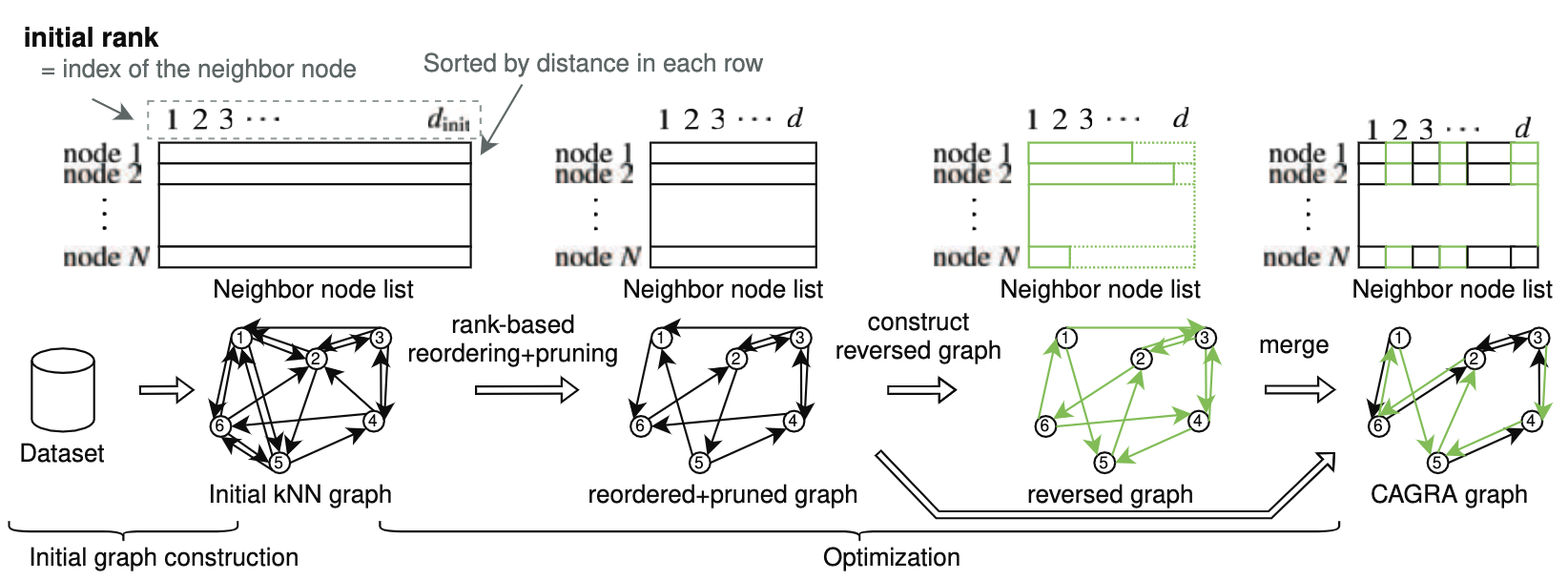
一、建立索引

（1）初始k-NN图构建

采用GPU加速的NN-Descent算法[11]构建基础k-NN图（k=2d~3d），其过程与CPU版NN-Descent存在关键差异：

• 批量反向邻居计算：

  将反向邻居关系​R(v_i)的计算转化为GPU友好的矩阵转置操作，利用共享内存（Shared Memory）加速原子操作。以d=64为例，单次迭代可并行处理​10^6节点的反向关系更新。

• 动态内存预分配：

  显存预分配策略消除动态扩展开销，每个节点维护固定容量（如128）的候选队列，超出部分截断处理。

（2）图结构优化

在初始k-NN图上执行两级优化以提升搜索效率：

1. 基于秩的重排序：

   对每个节点​v_i的邻居列表​N(v_i)，按原始距离排序生成秩次（rank），将低秩边（重要连接）前移。该操作在GPU上实现完全并行化，单卡可在1秒内完成百万级节点的秩次重排。

2. 反向边增强：

   为提升图连通性，对每条边​v_i → v_j添加反向边​v_j → v_i，但限制各节点出度不超过d（默认d=64）。反向边按源节点秩次动态截断，确保显存访问连续性。

二、检索机制

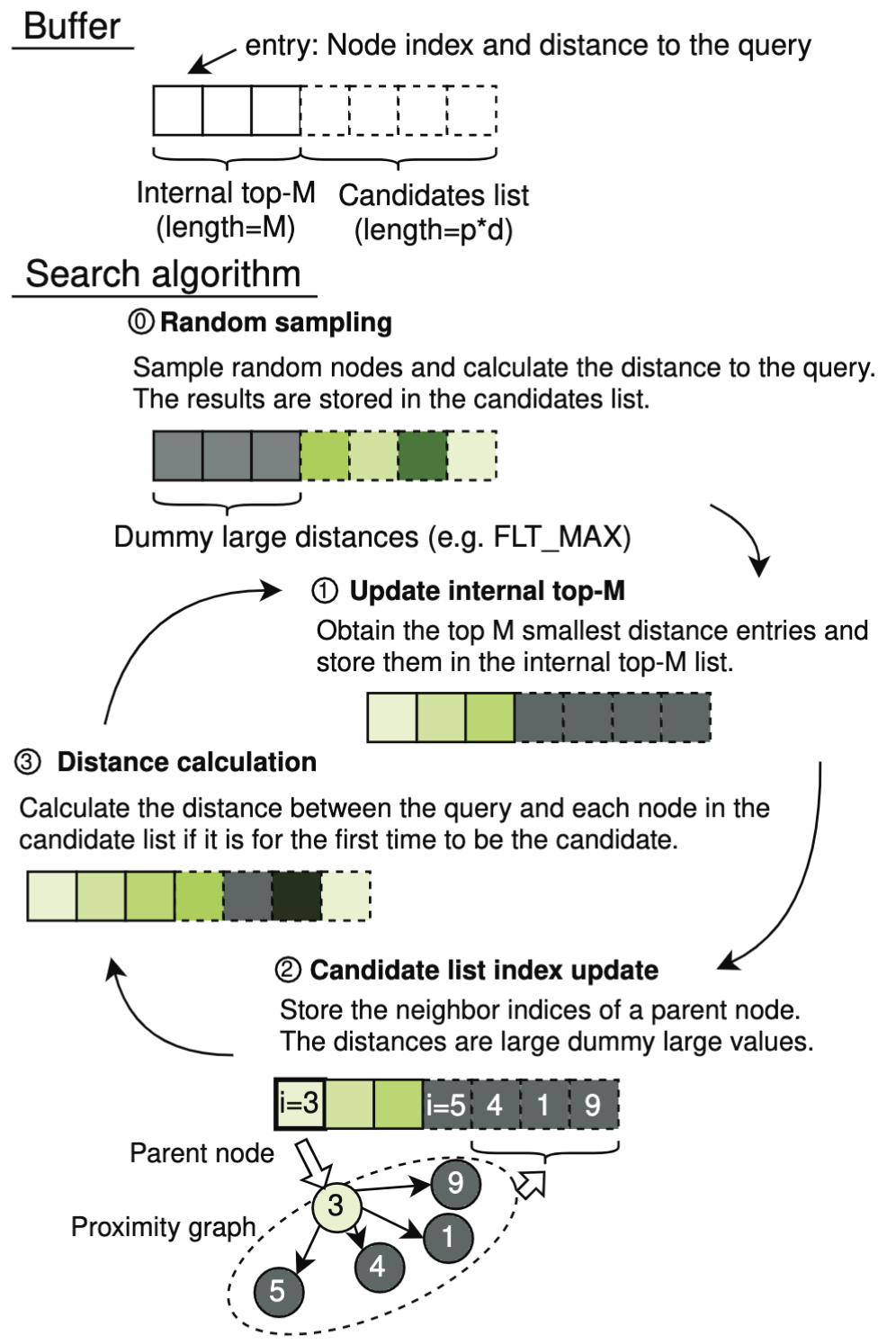
CAGRA[14]的检索流程针对GPU架构进行了系统性重构，其核心突破在于全流水线并行化与动态候选缓冲机制的设计。与HNSW等层次化图索引不同，CAGRA放弃逐层递进的串行路径优化策略，转而通过广度优先的并行扩展提升GPU线程利用率，具体实现如下：

（1）双缓冲架构设计

CAGRA采用Top-M Buffer与Candidate Buffer的双层动态缓冲机制（图8，Top-M Buffer有序存储当前最优结果；Candidate Buffer无序存储潜在候选），实现计算与访存的深度解耦：

• Top-M Buffer（有序区）：

  • 容量固定为​M（如​M=200），按距离升序排列当前最优候选节点。
  • 采用最小堆数据结构，插入复杂度​O(\log M)，支持动态替换。

• Candidate Buffer（无序区）：

  • 容量为​E（扩展因子，如​E=64），存储新扩展的候选节点。
  • 无序设计避免排序开销，通过原子操作实现并行写入。

（2）并行搜索策略

在GPU线程束（Warp）级别实现候选节点的批量扩展与距离计算，具体流程如下：

1. 随机种子采样：每个查询启动时，从全局图中随机选取​E个节点（如​E=64）作为初始候选，存入Candidate Buffer中。
2. 更新Top_M：将Top-M Buffer与Candidate Buffer合并，保留前​M个最近邻，存入Top_M Buffer。
3. 更新Candidate Buffer：在Top_M Buffer中选取没有被访问的离query最近的若干节点的所有邻居，放入Candidate Buffer。
4. 计算距离：计算Candidate Buffer中节点与query的距离。回到step2，直到计算至收敛（Top_M Buffer全部是已访问状态且距离query最近）。

为什么使用GPU加速向量检索？

在大规模向量检索场景中，传统的CPU架构逐渐显现出性能瓶颈。随着数据规模的指数级增长和向量维度的不断提升，计算复杂度呈爆炸式增长，尤其是高维向量的距离计算成为主要的时间消耗点。而GPU凭借其强大的并行计算能力，为加速向量检索提供了全新的解决方案。

1. GPU的并行计算优势

GPU拥有数千个核心，能够同时处理大量线程任务。对于向量检索中的高维距离计算（如欧氏距离、余弦相似度等），GPU可以将这些计算分解为细粒度的并行任务，每个线程负责计算一个或多个维度的差值与平方操作，随后通过高效的规约操作完成最终求和。这种高度并行化的计算方式使得GPU在处理大规模向量检索时，相比单线程为主的CPU具有显著的速度优势。

2. 显存带宽与数据吞吐能力

向量检索涉及频繁的向量加载与存储操作，这对内存带宽提出了极高要求。GPU配备了高带宽的显存，能够快速读取和写入大规模向量数据。此外，GPU的显存访问优化机制（如共享内存、缓存对齐访问）进一步提升了数据吞吐效率，减少了因内存延迟导致的性能损失。

3. 针对算法的硬件加速

现代GPU支持专门的数学运算指令集（如CUDA Core、Tensor Core），可以高效执行矩阵运算和向量操作。例如，在批量距离计算阶段，GPU可以利用Warp级别的协作机制，将高维向量的距离计算转化为并行的减法、平方和规约操作，从而实现数十倍甚至上百倍的加速效果。此外，针对特定算法（如乘积量化PQ、图索引搜索），GPU可以通过定制化优化（如固定度数图存储、Cuckoo Filter替代哈希表）进一步提升性能。

4. 支持实时性需求

在医疗病理学、推荐系统等实际应用场景中，向量检索往往需要满足毫秒级甚至微秒级的实时响应需求。GPU的高吞吐能力和低延迟特性使其能够轻松应对千万级甚至亿级向量数据库的实时查询任务。例如，基于GPU的索引方法（如SONG、CAGRA）能够在单次查询中并行处理数百个候选节点，显著缩短了检索时间。

5. 灵活性与可扩展性

GPU不仅适用于单一任务的加速，还可以通过多卡并行扩展进一步提升性能。对于超大规模向量数据集，可以通过分布式GPU集群实现跨节点的协同计算，满足更高的并发需求。此外，GPU的编程框架（如CUDA）提供了灵活的开发接口，使研究人员能够针对特定场景优化算法设计。

总结

综上所述，GPU加速已成为向量检索领域的核心技术之一。其卓越的并行计算能力、高效的显存管理机制以及针对算法的硬件优化，使得向量检索在面对海量数据和高维空间时依然能够保持高效性和实时性。无论是学术研究还是工业应用，GPU加速都在推动向量检索技术的快速发展，为人工智能和大数据领域提供了强有力的支持。

[1] Chen, Richard J., et al. "Towards a general-purpose foundation model for computational pathology." Nature Medicine 30.3 (2024): 850-862.

[2] Song, Kaitao, et al. "Mpnet: Masked and permuted pre-training for language understanding." Advances in neural information processing systems 33 (2020): 16857-16867.

[3] He, Kaiming, et al. "Deep residual learning for image recognition." Proceedings of the IEEE conference on computer vision and pattern recognition. 2016.

[4] Dosovitskiy, Alexey, et al. "An image is worth 16x16 words: Transformers for image recognition at scale." arXiv preprint arXiv:2010.11929 (2020).

[5] Devlin, Jacob, et al. "Bert: Pre-training of deep bidirectional transformers for language understanding." Proceedings of the 2019 conference of the North American chapter of the association for computational linguistics: human language technologies, volume 1 (long and short papers). 2019.

[6] Gu, Yu, et al. "Domain-specific language model pretraining for biomedical natural language processing." ACM Transactions on Computing for Healthcare (HEALTH) 3.1 (2021): 1-23.

[7] Bentley, Jon Louis. "Multidimensional binary search trees used for associative searching." Communications of the ACM 18.9 (1975): 509-517.

[8] Omohundro, Stephen M. "Five balltree construction algorithms." (1989).

[9] Han, Yikun, Chunjiang Liu, and Pengfei Wang. "A comprehensive survey on vector database: Storage and retrieval technique, challenge." arXiv preprint arXiv:2310.11703 (2023).

[10] Jegou, Herve, Matthijs Douze, and Cordelia Schmid. "Product quantization for nearest neighbor search." IEEE transactions on pattern analysis and machine intelligence 33.1 (2010): 117-128.

[11] Dong, Wei, Charikar Moses, and Kai Li. "Efficient k-nearest neighbor graph construction for generic similarity measures." Proceedings of the 20th international conference on World wide web. 2011.

[12] Malkov, Yu A., and Dmitry A. Yashunin. "Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs." IEEE transactions on pattern analysis and machine intelligence 42.4 (2018): 824-836.

[13] Zhao, Weijie, Shulong Tan, and Ping Li. "Song: Approximate nearest neighbor search on gpu." 2020 IEEE 36th International Conference on Data Engineering (ICDE). IEEE, 2020.

[14] Ootomo, Hiroyuki, et al. "Cagra: Highly parallel graph construction and approximate nearest neighbor search for gpus." 2024 IEEE 40th International Conference on Data Engineering (ICDE). IEEE, 2024.

[15] Fan, Bin, et al. "Cuckoo filter: Practically better than bloom." Proceedings of the 10th ACM International on Conference on emerging Networking Experiments and Technologies. 2014.